Uma Torre Surpreendente
Será que é
possível empilhar blocos semelhantes de tal forma que o bloco superior
esteja deslocado horizontalmente em relação ao bloco da base de
uma distância maior que seu próprio comprimento, como mostrado na
figura abaixo?
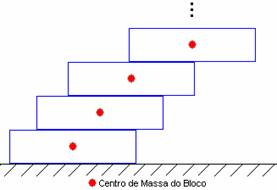
Sim, desde
que tenhamos uma quantidade suficientemente grande de blocos, certa
paciência e habilidade, podemos fazer com que o bloco superior esteja
tão deslocado do bloco inferior quanto quisermos.
Para
fazermos o empilhamento, comecemos assim: primeiro empilhemos dois blocos, o
superior o mais deslocado do inferior quanto possível, ou seja, alinhe
os blocos e depois os desloque até que o bloco superior esteja na
iminência de cair. Esse deslocamento será igual à metade do
comprimento dos blocos, neste caso o centro de massa do bloco superior
estará exatamente na borda do bloco inferior. Veja a figura a baixo:
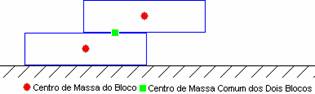
O bloco superior está deslocado em relação ao bloco
inferior de uma distância igual à metade de seu comprimento,
digamos, L/2 (onde “L” é o comprimento total de cada
bloco), e o centro de massa comum dos dois blocos estará
em no ponto indicado na figura, a uma distância igual a L/4 do extremo direito do bloco
inferior. O próximo passo é colocar esses dois blocos sobre um
outro, de tal forma que esse centro de massa comum das duas peças esteja
exatamente na borda do terceiro bloco. Feito isso, o extremo direito do bloco
superior estará deslocado em relação ao extremo direito do
inferior de uma distância igual a L/2 + L/4, assim como
você pode ver na figura abaixo:
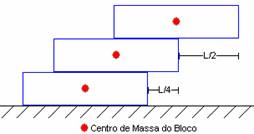
Agora, o centro de massa conjunto dos três blocos estará a uma
distância igual a L/6 do extremo direito do bloco inferior.
Próximo passo: colocar esses três blocos sobre um quarto bloco.
Feito isso, o extremo direito do bloco superior estará a uma
distância de L/2+L/4+L/6=11L/12. Veja:
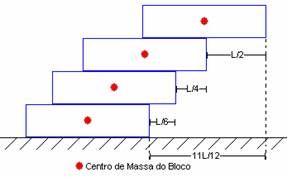
Podemos
perceber que a partir de agora, mais um bloco colocado e a distância
será L/2+L/4+L/6+L/8=25L/24, que já é superior
a L e, portanto, o bloco superior já estará deslocado em
relação ao bloco inferior de uma distância superior ao seu
comprimento.
Você
irá perceber que este procedimento pode ser continuado indefinidamente
sendo a distância total entre os extremos direitos do bloco superior e do
bloco inferior dada por
,
onde o número de termos na soma será igual ao número de
blocos menos um. Essa soma dentro dos parênteses cresce indefinidamente na
medida em que acrescentamos mais um número, ou seja, ela não
converge. Assim, podemos conseguir que o bloco superior esteja tão
deslocado do bloco inferior quanto quisermos, mas isso é claro, se
tivermos paciência e habilidade suficientes para conseguir fazer a pilha
de blocos crescer, pelo menos em teoria,
indefinidamente.
Tente fazer essa pilha usando alguns livros iguais – ou pelo menos
parecidos.
Explorando o infinito um pouco mais a fundo...
Há muitos séculos, operações
envolvendo quantidades infinitas, tais como as vistas no problema anterior,
desafiam a intuição humana. Não é raro sermos
surpreendidos quando analisamos certos tipos de problemas, aparentemente
simples, usando o devido rigor matemático.
Vamos
ilustrar este fato, propondo um problema um pouco diferente do da
“torre”: imagine que você se encontra a uma certa
distância de um obstáculo e deseja alcançá-lo. Na
prática, sabemos que isso é plenamente concebível e,
melhor ainda, a escala de tempo em que isso ocorre é da ordem dos acontecimentos
cotidianos. Certo? Agora veja como o fato simples de alcançar um
obstáculo pode nos trazer surpreza dependendo de como o problema
é abordado.
Por
volta do século V a.C., um filósofo chamado Zenão de
Eléia, propôs alguns “paradoxos” envolvendo movimento
e tempo. Em seus “paradoxos”, Zenão sugere que o movimento
é uma espécie de “ilusão”! Vejamos o
porquê de Zenão achar isso. Bem, ele diz que, no caso do alcance
do obstáculo, primeiro você deve percorrer a primeira metade da
distância total, depois mais metade da distância restante, e
então mais metade do que resta, e assim sucessivamente. De forma que
esse processo demoraria um tempo infinito, pois se para cada deslocamento
há uma demanda de tempo, seria impossível percorrer a
distância em um tempo finito. Portanto, o paradoxo surge ao supor
intuitivamente que a soma de infinitos intervalos de tempo é infinita,
de tal forma que seria necessário passar um tempo infinito para que
você pudesse alcançar o obstáculo. Mas, como resolver este
aparente dilema? Bom, a resolução deste “paradoxo”
envolve o conhecimento da convergência e divergência de
séries, que foi devidamente resolvida depois de cerca de 2
milênios depois da proposisão do filósofo. Basicamente, os
infinitos intervalos de tempo descritos no paradoxo formam uma
progressão geométrica e sua soma converge para um valor finito.
Pequena formalização do
problema da construção da torre...
Em nosso problema inicial, a soma
sucessiva das distâncias, de modo que o centro de massa
das figuras formadas a cada empilhamento coincidam com a extremidade do
bloco a ser adicionado, é definido, segundo o
“matematiquês” por uma série numérica.
Notação:
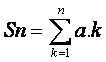
No caso da torre temos,
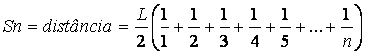
Este
tipo de série é definida matematicamente
por “p-série”. Denotada por:
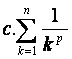; onde 
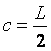e p = 1.
Pode-se
demonstrar que quando p>
1, a série diverge (a soma, via de
regra para nosso interesse, resulta em um número infinito).
“Tá bom, e em que
isso me ajuda?”
Traduzindo
agora do “matematiquês” para nosso idioma. Como foi dito
anteriormente, não temos um limite de crescimento horizontal para nossa
torre. O único limite para a nossa torre seria a falta de habilidade
manual, tempo hábil disponível para a construção e
uma quantidade grande de blocos.