Estimando Velocidades
Como estimar a velocidade de um carro que nos ultrapassa?
Às vezes um carro nos ultrapassa a alta velocidade e ficamos curiosos
para saber quão depressa ele estava,
principalmente se o limite da estrada é a velocidade do nosso carro.
Aqui vai uma sugestão de como estimar essa velocidade.
No
momento em que o carro em alta velocidade o ultrapassa, comece a contar o tempo. E você não precisa de um
cronômetro para isso (o importante é ter certeza que os intervalos
de tempo sejam semelhantes): basta começar a contar de forma regular,
um, dois, três.... Quando chegar a dez, observe
onde o outro veículo está: você pode fazer isso observando
uma placa, uma árvore, uma sombra, ou qualquer outra coisa que sirva
como uma referência fácil e que, se você estiver dirigindo,
não tire sua atenção da estrada. Mas não pare de
contar: onze, doze, treze··. Quando o veículo em que
você está passar por aquela referência que você
marcou, pare de contar. Digamos que você chegou ao número N,
aí basta multiplicar a velocidade do seu veículo Vo pelo número que você chegou dividido por
dez:
.
Como vemos na equação acima, V
é a velocidade do carro que nos ultrapassa e Vo
é a velocidade marcada pelo velocímetro do veículo em que
você se encontra. Por exemplo, se você chegou a 13 e a velocidade
do carro em que está é de
Deduzir a fórmula acima é muito simples, usando cinemática
elementar. O seu veículo e o outro veículo andaram exatamente a
mesma distância (S) desde que você começou a contar
até que você chegou no ponto de referência. Só que o
seu veículo percorreu essa distância num tempo N/10 maior.
Portanto, a velocidade do outro veículo é N/10 maior que a
do seu. Veja como isso ficaria na ilustração abaixo:
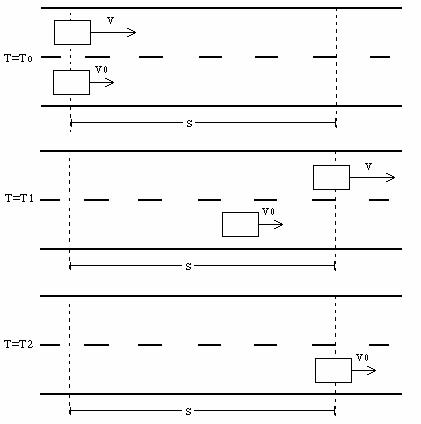
Aqui estão as
equações dos dois veículos:
e 
, igualando a distância(S), temos:
, o que dá:
E, finalmente, no caso da
equação (1), T1 é o tempo que o carro que nos ultrapassa
leva pra chegar ao obstáculo arbitrário; e T2 é o tempo
que o carro em que você estiver leva para alcançar o mesmo obstáculo.
Algumas vezes, quando fazemos isso em estradas, o
veículo que ultrapassa está tão rápido que nem
podemos esperar o dez para
determinar o ponto de referência, pois ele já teria desaparecido
em um a curva ou estaria muito distante para observar com detalhe uma boa
marca. Nesse caso, marque a referência no 5. E assim teríamos T1=5
e T2= ao tempo que o nosso carro leva a atingir o obstáculo.
E qual a sua velocidade?
Em
geral, a velocidade que é marcada pelo cronômetro dos carros
é uma superestimação da
velocidade real. Porém, esse “erro” é pequeno e pode
variar de carro para carro.
Você
pode verificar o quanto o velocímetro está diferindo da
velocidade real. Para isto, basta você medir o tempo, em segundos, entre
duas marcas sucessivas de quilometragem na estrada (geralmente essas marcas
são colocadas a cada quilômetro). A velocidade de seu
veículo será de
Por exemplo, se t for de 60 s, a velocidade
será de
Você pode achar que dividir 3600 por algum
número é uma tarefa que exige, pelo menos, papel e lápis.
Mas, não. Por sorte 3600 é divisível por vários
números inteiros, como 60 (e neste caso a velocidade será de
E agora a
atividade anterior (medir a velocidade de um carro que nos ultrapassa), pode
ficar um pouco mais precisa. É só você estimar a velocidade
real que o seu veículo acusa, e aplicar na equação do
problema anterior.
E se Doppler fosse músico?
Essa nossa próxima atividade
tem certa dose desafiadora aos que possuem “bom ouvido musical”.
Mas, antes de propor o “desafio”, descreveremos, de forma
básica, o fenômeno em que será baseado nosso texto.
Começando:
na prática, o fenômeno em questão consiste na ligeira
diferença de tom percebida quando uma ambulância, por exemplo,
passa por nós com sua sirene ligada (muitas vezes a sirene, por ser um
som intermitente, torna o problema de reconhecimento da mudança de tons
um trabalho difícil; por isso pode-se pensar na diferença de tom
provocada pelo barulho do motor, que tem som contínuo e mais fácil
de perceber a mudança). E com “passa” eu quero dizer:
inicialmente a ambulância está se aproximando, e depois, se
afastando. É a manifestação dessa
“diferença de tons” que damos o nome de Efeito Doppler.
Agora que já sabemos o
comportamento do fenômeno na prática, vamos tentar quantificar e
dar uma noção de como descrever matematicamente o Efeito Doppler.
Para isso, imaginemos primeiramente, uma fonte imóvel emitindo pulsos
sonoros (ondas de pressão tridimensionais) conforme a figura abaixo:
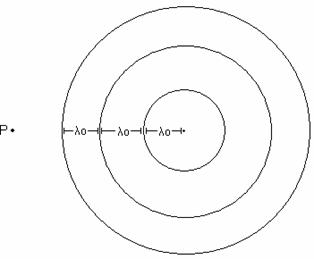
Figura 1:
Representação, no plano, de um conjunto de pulsos sonoros.
Na
figura, denotamos a distância entre dois pulsos como comprimento de onda λo, e para um observador situado em “P”,
definimos um tempo To, correspondente ao período de
propagação da onda sonora. Com estes dois parâmetros em
mãos, usando uma relação simples da cinemática
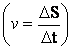,definimos a velocidade de propagação de uma
onda sonora como:
. E como, por
definição,
, ou seja, a freqüência (fo)
é igual ao inverso do
período, podemos escrever (1) como:
.
Agora,
levando em conta as definições feitas anteriormente, imaginemos
um observador em repouso no ponto “P” e uma fonte emissora de ondas
de pressão (sonoras) se aproximando de “P” (referencial
fixo) com velocidade de magnitude V, conforme pode-se verificar na figura
abaixo:
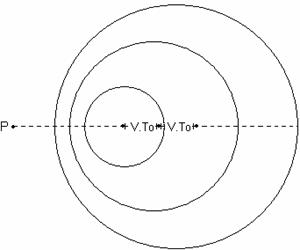
Figura 2: Representação no plano do
movimento da fonte sonora em relação ao ponto “P”,
evidenciando o deslocamento S=V.To devido a velocidade de
aproximação V.
Como pôde ser visto na figura, a cada
período To a fonte se locomove de uma S= V.To, aproximando-se de
“P”. Portanto, lembrando da relação, na
situação de fonte e observador em repouso, definido acima,
podemos concluir que o comprimento de onda resultante λ pode ser escrito
como:
,ou ainda, 
. E finalmente, usando a relação (2), podemos
reescrever (4) como:
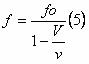
que é a equação, para
aproximação da fonte sonora, que nos permitirá a
manipulação dos dados a serem propostos no desafio. Agora,
para o afastamento, quando a fonte
“passa” pelo observador, podemos perceber que (5) será igual
a menos de um sinal, ou seja:
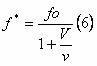
. Finalmente,
com estas duas últimas equações em mãos, poderemos
propor o nosso “desafio”...
Será
que você teria condições de estimar a velocidade de uma
ambulância (V) apenas ouvindo a
diferença de tom entre o som emitido na aproximação da fonte
quando comparado ao som do afastamento, assim que a fonte emissora passar por
você?
Aos
que aceitaram o desafio, aqui vai uma sugestão de procedimento:
suponhamos que, de alguma forma (no caso esse é o ponto que se precisa
de um “bom ouvido musical”), você consegue perceber a nota
musical Lá (freqüência f=440hz)quando
a ambulância se aproxima e a nota musical Sol (freqüência f*=392hz) quando se afasta. A partir
daí, você terá que fazer alguns cálculos
através das expressões (5) e (6), usando o valor aproximado para
velocidade de propagação do som no ar (v)
de 340m/s (1224km/h). Resolução:
Usando o fato de que fo é igual tanto para
aproximação quanto para o afastamento, podemos fazer:
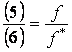, que
substituindo em valores dá:
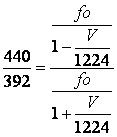
isolando e V concluímos que:
que é uma velocidade bem comum para uma
ambulância. Agora é sua vez, tente descobrir as notas e estimar a
velocidade sozinho, boa sorte!
Observação:
Você deve ter notado que na equação acima, onde fizemos a divisão de (5) por (6), o que importa realmente
para o cálculo da velocidade da fonte emissora de ondas sonoras é
a relação entre as freqüências de aproximação
e de afastamento. Sendo assim, segue uma tabela abaixo para com a relação
de freqüências relativas a mudança
de tom da fonte emissora quando passa por um observador e a velocidade para
alguns tons comuns. Note também que a tabela tem valor de velocidade até
uma diferença de 4 tons, e isso porque a
velocidade para essa diferença é muito elevada.
|
Tabela Para Freqüências Relativas E
Velocidade Aproximada |
||
|
Variação [tons] |
Relação (aproximado) |
Velocidade [km/h] |
|
meio
tom |
1,06 |
36 |
|
um
tom |
1,12 |
69 |
|
um
tom e meio |
1,19 |
106 |
|
dois
tons |
1,26 |
141 |
|
dois
tons e meio |
1,33 |
173 |
|
três tons |
1,41 |
208 |
|
três tons e meio |
1,50 |
245 |
|
quatro
tons |
1,59 |
279 |